How many bottle caps?
I ran across the following problem and couldn't resist. The original inspiration was a Mountain Dew promotion.
Consider the following game: Suppose you have N bottle caps, each with the name of a different sports team on the underside. You win if you draw (with replacement) three of the same team. Note that a win is impossible for less than three draws and is guaranteed by the 2N+1 draw. For n draws, the probability of having some particular set of caps  ,
, 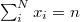 , follows a Multinomial distribution:
, follows a Multinomial distribution:
The probability of not winning by the n'th draw is the sum of all the probabilities with
 ,
,  , and
, and 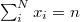 . Now, permutations of the vector
. Now, permutations of the vector  are equally likely, and the number of possible non-winning vectors that have
are equally likely, and the number of possible non-winning vectors that have 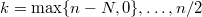 teams with two drawn caps is
teams with two drawn caps isThen, the probability of not winning by the n'th draw, given that there are k teams with two caps, is
Thus, the probability of winning on the (n+1)'th draw is
If there are 30 teams, the chance of winning on the third draw is 0.1%. It takes about 18 draws to have a 50% chance of winning, 27 draws to have a 90% chance of winning, and 38 draws to have a 99.9% chance of winning.