Calculating a Graduated Annuity

(Use the calculator to skip the math below.)

Calculating the future value of a savings program with fixed savings installments and a fixed interest rate (a simple annuity) is fairly straightforward with a geometric series:

To calculate the value after periods, we multiply the last equation by and subtract the result: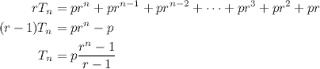


So, saving $1,000/year for 10 years at 5% interest would give:


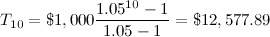
And if we had the goal of saving $100,000 over 30 years with a 8%
interest rate, we could calculate the yearly deposit required:



Now, since the real value of the periodic deposit degrades over time due to inflation, and since one's ability to save will hopefully increase over time due to increased income through cost-of-living increases and promotions, a real-life long-term savings plan will likely include deposits that increase over time (a graduated annuity). These, too, can be represented with a series:


where is the geometric ratio describing the rate of increase (the graduation) of the deposits. This series is similar in form to the binomial series, except that the coefficients in this series are all the same. To solve for the sum, we multiply by and subtract:


Notice how this simplifies to the result for constant deposits, when .

This equation can be rearranged to the elegant form:


When asked to solve for either rate, Mathematica complained that this equation involves variables in "an essentially non-algebraic way," which I found a bit odd. Nevertheless, to determine the interest rate necessary to achieve a given sum with a set rate of deposit graduation (or vice versa), one can evaluate one side of the equation, move the resulting constant to the other side, and calculate the positive real roots of the n-th degree polynomial.

In any case, after 10 years, a savings program that begins at $1,000/year
and increases by 4% each year with 8% interest would give:



This equation is also useful for determining savings left after a series of increasing withdraws. If one starts with $500,000 in retirement savings invested at 5%, taking a 2% inflation-adjusted $30,000 annuity for 5 years would leave:



One can rearrange the formula to achieve a somewhat unwieldy but functional equation for the number of years before the retirement savings will run out:


So, to find out how long the $500,000 investment from the previous example will last:



All of these calculations assume that payments occur at the end of the year (an ordinary annuity). The calculations for payments at the beginning of the year (an annuity due) are equally straightforward, and yield:

Because We Were Slaves

When you are harvesting in your field and you overlook a sheaf, do not go back to get it. Leave it for the alien the fatherless, and the widow, so that the Lord your God may bless you in all the work of your hands.

When you beat the olives from your trees, do not go over the branches a second time. Leave what remains for the alien, the fatherless, and the widow.

When you harvest the grapes in your vineyard, do not go over the vines again. Leave what remains for the alien, the fatherless, and the widow.

Remember that you were slaves in Egypt. That is why I command you to do this. (Deuteronomy 24:29-22)

What would people say if you were to ask them why they should give to the needy? "It's their human right to have adequate food, shelter, clothing, and education," some might say. "It's your social responsibility," perhaps. Or maybe, "What goes around comes around."

Do you think anyone would say, "Because we were slaves"?

I find it striking that God gave precisely this reason for his command of charity to the Israelites as they were poised to cross the Jordan into the Promised Land. Why, of all things, would God ground his command in their former slavery?

Some might suggest that God was calling the Israelites to recall their former meager estate in order to identify with the poor, and thus to give out of empathetic pity. And, while this certainly could be part of it, I think there's something much more to God's reasoning here.

Not only were all the riches the Israelites possessed--from the spoils of Egypt to the land they were soon to inherit and its abundant fruit--gifts directly from God, but the Israelites would be in no position to enjoy any of these material goods if not for God's mighty deliverance of them from the bondage of slavery in Egypt. In recalling for them their former slavery, God is saying, "Remember how it is you got the land for your fields and vineyards; remember why you are free to cultivate and harvest. The only reason you live in comfort is because I have saved you and given you all you have." God commanded the Israelites, therefore, to give of their goods (which were really God's to begin with) to the poor among them in thanksgiving to God for his provision and liberation, providing a kind of miniature liberation in turn for the poor from the bonds of poverty.

"Now that's all well and good for the Israelites," you might say, "but I worked hard for my own riches, and have been enslaved to no man." Not so fast. Whatever work you have done to earn your income you would not have accomplished without the gifts of God--even the gifts as basic as your latent abilities and drive for hard work. But more importantly, you, as well, were also a slave--a slave to sin and death. By trusting in Jesus Christ, you accept the gift of liberation from the bondage of the slavery to death. And in thanksgiving for this salvation, God calls you to share his gifts with the poor.

So, when asked why charity is important, you too can say, "Because we were slaves."


For more Biblical insights on poverty, I commend to you the sermon series on poverty given at Blanchard Alliance Church, in Wheaton, Illinois:
The Dignity of Potato Eaters, 1/7/2007
Stopping Our Oppression of the Poor, 1/14/2007
Living on Less to Share with Others, 1/21/2007
Helping the Poor Regain the Dignity of Self Support, 1/28/2007